Perfect numbers are integer numbers which are equal to the sum of their proper divisors. For instance, 6 has the proper divisors 1, 2 and 3. And 1+2+3 = 6. So 6 is a perfect number. In fact, it's the smallest one there is. What are the next perfect numbers? Well, let's ask Python.

To check, if a number \(n\) is a perfect number, we have to determine its divisors, then sum them up and see if the result agrees with \(n\).

To get the divisors, we can use the divisors function from sympy:

from sympy import divisors

divisors(6)

[1, 2, 3, 6]

But we only need the proper ones, so we skip the last entry:

divisors(6)[:-1]

[1, 2, 3]

and sum the entries using Python's builtin sum function:

6 == sum(divisors(6)[:-1])

True

Which perfect numbers are in the range from 1 to 100000? I'd guess many...

from sympy import divisors

perfect_numbers = [
    n for n in range(1, 100000) if n == sum(divisors(n)[:-1])
]

perfect_numbers

[6, 28, 496, 8128]

Oh, so few! What's the next one? It turns out that this brute force approach is getting too time consuming to get even the next perfect number.

Fortunately, there is an explicit formula which can give us all the even perfect numbers. If there are odd perfect numbers is still unknown. Jacques Touchard made an observation about odd perfect numbers in 1953, noting that any odd perfect number, if it exists, must have at least nine distinct prime factors. Other mathematicians have further refined this bound over the years. But as I said, the problem is still open. In fact, this is one of the oldest unsolved problems in mathematics!

The formula for even numbers is

$$ 2^{p-1} \left(2^p - 1\right) $$

where \(p\) must be a prime number. Amazingly, this formula was already known to Euclid in 300BC! That's amazing because he had to establish that formula from the only 3 perfect numbers known at that time: 6, 28 and 496. So, Euclid had a formula that produced even perfect numbers. But does it generate all even perfect numbers? Yes, it does! This was not proved by Euclid but only much later by Euler in the 18th century.

Now, let's compute the first 100 even perfect numbers using the formula above. The formula requires \(p\) to be a prime number, so we first need to calculate the first 100 prime numbers and then apply the formula to them.

from sympy import isprime

primes = []
n = 2
while True:
    if isprime(n): primes.append(n) 
    if len(primes) == 100: break
    n += 1

Having the first 100 prime numbers, we can determine the first 100 even perfect numbers:

perfect_numbers = [
    2**(p-1) * (2**p - 1) for p in primes
]

perfect_numbers

[6,
 28,
 496,
 8128,
 2096128,
 33550336,
 8589869056,
 137438691328,
 35184367894528,
 144115187807420416,
 2305843008139952128,
 9444732965670570950656,
 2417851639228158837784576,
 38685626227663735544086528,
 9903520314282971830448816128,
 40564819207303336344294875201536,
 166153499473114483824745506383331328,
 2658455991569831744654692615953842176,
 10889035741470030830754200461521744560128,
 2787593149816327892690784192460327776944128,
 44601490397061246283066714178813853366747136,
 182687704666362864775460301858080473799697891328,
 46768052394588893382517909811217778170473142550528,
 191561942608236107294793378084303638130997321548169216,
 12554203470773361527671578846336104669690446551334525075456,
 3213876088517980551083924184681057554444177758164088967397376,
 51422017416287688817342786954912132678309582883443383916822528,
 13164036458569648337239753460458722910223472318386943117783728128,
 210624583337114373395836055367340540119236532374371439352601378816,
 53919893334301279589334030174039256154977430310253516431710891278336,
 14474011154664524427946373126085988481573677491474835889066354349131199152128,
 3705346855594118253554271520278013051303278379832814295408789189823493075632128,
 15177100720513508366558296147058741458143716317808908249533137827185687195503558656,
 242833611528216133864932738352939863330300506432373713115489964721765025520002531328,
 254629497041810760783555711051172270131433548851430108153027585904726170108043304177238016,
 4074071952668972172536891376818756322102936785904624808566321017650476630077178275984048128,
 16687398718132110018711107079449625895333629080820005912878081128723361305616486608325895520256,
 68351585149469122636640694597425667667286544715407042631756007838638216485649632468656163051798528,
 17498005798264095394980017816940970922825355447145605955301375673492858957765713543674847436501680128,
 71671831749689734737838152978190216899892655911508779130488944723462986915472075446292831273991731675136,
 293567822846729153486185074598667128421960318613539983455287486225053913549739298645385078893411307333091328,
 4697085165547666455778961193578674054751365097816639739882086402198529191870869859777088813150798283880267776,
 4925250774549309901534880012517951725634967408808180833491967400096868551246192379070981365256588866239712490160128,
 78804012392788958424558080200287227610159478540930893335890309706756056862230585433405324843353728926168791946100736,
 20173827172553973356686868531273530268200826506478308693989425789346043360114350460413332999838419170405882106484883456,
 322781234760863573706989896500376484291213224103652939103832017833069888004536263838182583869366598378739450798384611328,
 5415370496329716522614090203404460358274291162843391748379842929242427684486656502844980829364797108488731343275411487879856128,
 90854840536950861318665475986000566794205170085914757535186274897573171027507952755825214585448690787426905914677637098571549301014528,
 23258839177459420497578361852416145099316523541994177929007686373780349379842064943878934954780086019421706142822827531583182837674672128,
 372141426839350727961253789638658321589064376671906846864122981980486884154913062332773103293205553253019632868097522452810018376086716416,
 95268205270873786358080970147496530326800480428008152797215483387004745869852945815646725964398555788154812780867548303717692142141556391936,
 390218568789499028922699653724145788218574767833121393857394619953171466910758936320442180487112121209248737433304853643026257429509485340131328,
 6243497100631984462763194459586332611497196285329942301718313919250743475872684175462227876543686441576735346415329348915276993236970369319960576,
 6546781215792283740026379393655198304433284092086129578966582736192267592807539858372207119098315017661012619694912798508033879278654261356533412528128,
 26815615859885194199148049996411692254958731641184786755447122887443528060146978161514511280138383284395055028465118831722842125059853682308859384882528256,
 109836762562089755439710412785302291476310964802292886550311415346968690934362489423267243062346765771093700426237591119314933206999367775715807946217543958528,
 449891379454319638281053850768598185886969711830191663310075557261183758067148786557619671094341949260045336467766418945326969415085679663282587421674337380335616,
 7198262071269114212496861612297570974191515389283066612961208916178940129074380590613327507702036825620086438631290749929157796926935878279940567903735546147504128,
 29484081443918291814387145163970850710288447034503440846689111720668938768688662906801448234686351054485255310751372606614307264980528722363647929480636420015685369856,
 7547924849643082704483109161976537781833842440832880856752412600491248324784297704170310781463091806012017288154704170892898762420797445743871056093126487802093582155776,
 120766797594289323271729746591624604509341479053326093708038601607859973196548763266748284530116177645043310153357148961166089080801384806156958646406890656255959816470528,
 126633165554229521438977290762059361297987250739820462036000284719563379254544315991201989386184656478087733284004292992614457290266643861939904583988539011421350466806125428736,
 33992831540273094316133645219357992149093959534530043084764424844825827831094543535306400144844303980323509977598595540923980875302479286127589358600348601765724798148611616822293168128,
 8702164874309912144930213176155645990168053640839691029699692760275411924760203145038438437111430691559316260550323784250507152631185251775371656611460359354108845090409425713484034736128,
 139234637988958594318883410818490335842688858253435056475195084164406590796163250320615014993807922163026258333833247208627288880941964472027313530431182643507408158858042692861326142734336,
 35644067325173400145634153169533525975728347712879374457649941546088087243817792082077443838416830561580897986663556618258119908628582940328701625762208108245229819660578279888146019496493056,
 9568131466127621947163770315237577352582483950433331955534014747297500715462012198465648064079848063601328552023870734107923211366220577195742134298765644503550440725370979161220276554505172578992128,
 39191066485258739495582803211213116836177854260974927689867324404930562930532401964915294470471057677330036671414878605975982453494288829297738927449176623555249690256050023416241975204458316640504774656,
 41094811730846668025320233460001005199612029709556045777330319555224469955445943922763019814668659775210661100525392946413488638148604587246886267583894801570041585628229290743616842807966895069112595673776128,
 657516987693546688405123735360016083193792475352896732437285112883591519287135102764208317034698556403372297732368279696249526326049149961155777705084193035963468561681208844054935848533522835020634125045334016,
 168324348849547952231711676252164117297610873690341563503944988898199428937506586307637329160882830439263445829403239006530575388722300515272326886400903514074072207120752679450628886313066046878468943552798785536,
 689456532887748412341091025928864224451014138635639044112158674527024860928026977516082500242976073479223111106781345658622576051525942342613632093698246099685363400199404607321921473421303081273433352899336578531328,
 45184223339331479951185741475274045813621662589625240394934430893803101285779175998493982735923679951534365847822237219952447423269127496967507279663747454572760265738456835751100735552548316061903381855036155491807920128,
 185074578797901741880056797082722491652594329967104984657651428941017502866551504889831353286343393081484762513285920369324846762500770916619204658742949704310720174460994219858452087336012382208476851213420887174429997531136,
 758065474756205534740712640850831325809026375545262017157740252942407691741394964028749223060862538061761587254457916182604148154677744854570841152050497357201074258655993925860024132097124284221532100914824292700384294315491328,
 194064761537588616893622436057812819407110752139587076392381504753256369085797110791359801103580809743810966337141374300269898406894548729170510873476696372465739255640939251120432099273506931300505021332650837364951404199729430528,
 794889263257962974796277498092801308291525640763748664903194643469338087775424965801409745320266996710649718116931108851127749840275117571954833482523263861996852620275528464469041358311830059795164872958922753841806884683105976713216,
 52093862756873861516248842115009826540193424393093032503095764154406540920450250558761189069309017896429139926511197190822115645542375752836843770908646367589511806538126769186076589324895570692142464524208779497973344504298836605540499456,
 13336028865759708548159703581442515594289516644631816320792515623528074475635264143042864401743108581485859821186866480889195353430151821571070792932658648217860609366198805604095497215282980427441088837642127850683243664639049750609580261376,
 873989987746428259412194333913416701987357762822590714399458303903535888835232670878457161432636363996257309241302481691722875954439943171214433889183073784761956089579096634987587948295758882058038591249137739484504454441920523522330408377122816,
 916444925391198758541401085877594831703095653509460880942126390473954048171292933099049096506388108013739504295007991042380698867305036013199675506568791122298867193568939431848569092886960959848311054280597722925478287446963918742290367563488273891328,
 14663118806259180136662417374041517307249530456151374095074022247583264770740686929584785544102209728219832068720127856678091189999936320705769592026235963063472412508539775174664728055955771689471339580283381066732670482372842907077459244502839224958976,
 15375394465392026070980930960402958051966483647589383243116337952281869440244186537876296086692518667977838631290276787444086150481814324505966657077220111583618277034029731403009598285402490223816697256890238955324094128259374517762862718279663124191146672128,
 246006311446272417135694895366447328831463738361430131889861407236509911043906984606020737387080298687645418100644428599105378407742301228424916291550462755547609436985712947352663371468485598548442611803911330761665198925399667221374498024011452849006036647936,
 1007641851683931820587806291420968258893675472328417820220872324040744595635843008946260940337480903424595632540239579541935629958157183448455237632245976110684867907862503089508170339259266506330573550401109940848169362020084600054304669356736427675986421327331328,
 257956314031086546070478410603767874276780920916074961976543314954430616482775810290242800726395111276696481930301332362735521269288409315630547616719942382102799935475539925608002697020750699886059791235835722495410932704652695949580299071325994120505696032053526528,
 1056589062271330492704679569833033213037694652072243044255921418053347805113449718948834511775314375789348789986514257357764695119005370347662353661318988604492965479993475814696102348034792600615849285177134263410372730394452409714111233035012466686801143627193847382016,
 69244620785013915169893880288577664649638356718206520148356066053544201755915040781030818563707002931730762300556198370198467059319135998552431931565419052243909164625788433597631789148931143049640501265501399129478621992882623717509553574759987473842295249890570297992544256,
 17726622920963562283492833353875882150307419319860869157979152909707315649514250439943889552308992750523075148942386782770807567185698815674079545701469364729791200900840837591681463222755194244402726161626836038833695639339129827536079183191806120792621556208351920348175794176,
 283625966735416996535885333662014114404918709117773906527666446555317050392228007039102232836943884008369202383078188524332921074971181050820998308200087505560939578218764600339453591724586165209399424856156158910688864956755019765260173705511497394673140077122723464820480278528,
 72608247484266751113186645417475613287659189534150120071082610318161164900410369802010171606257634306142515810068016262229227795192622349013033613057348615014342961128428633596704133894334302877522717264786119264284328207115600461881237010566351289995619473966544626134016357040128,
 1218164251424999885044172798484398538859528357199375940858488307151618586345803262808201883235251282403163114528926083522932396233150386755822247631601944098443351867095251680442272269786721039801312234395662391016275994799269329291692529578940830744870686998732310831391308751677662691328,
 79833612381388792466254908521473542642698050417418301660101889697488475674758562631398318619705428043573697873767699809758897519535743746429566871731601349592576724109621204353938865289864238356747980614795711543709441133739835127855963614674435612071361244505006376357023896334763500794544128,
 20437404769635530871361256581497226916530700906859085224986083762557049772738192033637969566644589579154866655684531151298277765001150399085969119211240003228553282046084361764231383970503712490661439914584353055035326838508997717779028428411892193705210140618087360021479023895567518508020400128,
 1339385758982834151185531311325002263201756014631917009304687985462938813906170153116497973519619822659493341146941433531483931607115392554498072196836503502839846936385525575753427425844742232223233506571759986530923709209323677306174875470178156825033677888678927753205249414820106700091318576611328,
 342882754299605542703496015699200579379649539745770754382000124278512336359979559197823481221022674600830295333617006984059886491421540493951506482390341300163474584226895338774687076965387009971910361569739554034002237585371141863673764325905162396637674740549459109081096885586700438806577267267862528,
 1404447761611184302913519680303925573139044514798677009948672509044786529730476274474284979081308875165000889686495260606709295068862629863225370551870890758713316045969442880344548702769352142847863423538577999846457819595548611664828896058956577358874445237732193799621409499276697036970904569222126370816,
 23562723457267347065789548996709904988477547858392600710143027597506337283178622239730365539602600561360255566462503270175052892578043215543382498428777152427010394496918664028644534128033831439790236838624033171435922356643219703101720713163527487298747400647801939587165936401087419375649057918549492160555646976,
 377003575316277553052632783947358479815640765734281611362288441560101396530857955835685848633641608981764089063400052322800846281248691448694119974860434438873355097911482282748203950843029662340260401218844363199341538461404774350013467723351797640748685740228608901743540130640130638008684789572236044315580694528,
 25907488423335759149119404380021415302343251169810191149683373827511083464703404402170929113783951935383945966632551924657895518385381565038977715192414529269954226708269458620094657942557125542893203167086816727242630477273902575953052692332796167979074804120896202565970170254033405757507005525666937594891241898728883224576]

Wow, the next perfect number after 8128 is already greater than 2 millions and the sequence increases very fast. By the way, note that we have made use of a nice Python feature which is built-in: it can handle arbitrarily large integers! That's not possible in most other languages without dedicated libraries.

Ok, how fast does the sequence increase? Let's make a semi-logarithmic plot of the first 80 numbers. We can't use all 100 because the numbers are too big to fit in a double variable when applying the logarithm.

import matplotlib.pyplot as plt

plt.semilogy(perfect_numbers[:80])

[]

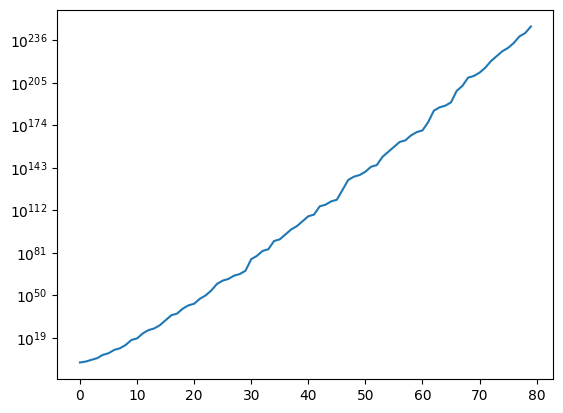
Well, that's almost linear, so the scaling is exponential, as we could have guessed from the explicit formula. However, since the density of prime numbers goes down like \(1/log(n)\), it is not completely obvious.

Wrap up

Perfect numbers, integers equal to the sum of their proper divisors, have long fascinated mathematicians and have a rich history dating back to Euclid's time. This article has explored the discovery, properties, and computational aspects of these numbers, showcasing Python's capabilities in handling large integer computations and mathematical libraries like sympy.